Ángulos adyacentes
Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.[1][2][3]
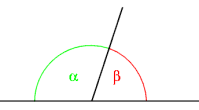
Ángulos adyacentes internos
editar- Los ángulos complementarios, dos ángulos cuya suma de medidas es 90°.
- Los ángulos suplementarios, dos ángulos cuya suma de medidas es 180°.
- Los ángulos conjugados, dos ángulos cuya suma de medidas es 360°.
Equivalencias: 360 grados sexagesimales equivalen a 400 grados centesimales, o 2π radianes. El ángulo cuyos lados están en línea recta recibe el nombre de ángulo llano.
Propiedades
editar- Los senos de los angulos adyacentes son los mismos, por ejemplos:
- sin( 120° ) = sin( 60° )
- sin( α° ) = sin( 180° - α° )
- sin( α ) = sin( π - α )
- Los cosenos de los ángulos adyacentes son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:
- cos( 120° ) = - cos( 60° )
- cos( α° ) = - cos( 180° - α° )
- cos( α ) = - cos( π - α )
Adjacent angles en inglés
editarEn idioma inglés se denominan adjacent angles a cualquier par de ángulos consecutivos, aunque éstos no sean suplementarios. Esto puede llevar a malinterpretar el concepto, o incluso provocar errores de traducción que eventualmente pueden encontrarse en artículos en nuestro idioma.[4]
Por lo tanto, debemos tener claro que en español, para que dos ángulos sean considerados adyacentes, es necesario que sumen 180°. Así entonces, los ángulos que muestra la figura no son adyacentes.
Véase también
editarRelaciones aritméticas entre ángulos:
Relaciones posicionales entre ángulos:
Determinados por dos paralelas y una transversal
Referencias
editar- ↑ Principios y ejercicios de geometría. (Acisclo Fernández Vallín y Bustillo, 1864) pág. 12.
- ↑ Geometría: El Encanto de la Forma. pág. 12.
- ↑ Notas de clase. Geometría en el plano y en el espacio. (Ana Berenice Guerrero G., Univ. Nacional de Colombia) pág. 32.
- ↑ Adjacent Angles en inglés. Demostración animada interactiva.
Enlaces externos
editar- Complementary Angles animated demonstration. With interactive applet
- Supplementary Angles animated demonstration. With interactive applet
- Angle definition pages with interactive applets that are also useful in a classroom setting. Math Open Reference